Discrete Structures & Optimization MCA paper Dec 2020

Subject Code: - PGCA 1917
Subject Name: - Discrete Structures & Optimization
Date of Examination: - December 2020
Class: - MCA 1st

Instructions to Candidates

Section A is Compulsory consisting of TEN questions carrying TWO marks each.
Section B & C have FOUR questions each.
Attempt any FIVE questions from SECTION B & C carrying TEN marks each.
Select at least TWO questions from SECTION B & C

SECTION-A

What are ordered pairs?
Write the concept of Hashing Functions?
Discuss rings in discrete structure.
What is meant by isomorphic in graph theory?
Give an example of a Finite graph.
Write about the principle of Inclusion.
Define an undirected graph.
What is the Indegree of the graph?
What is the use of the Karnaugh Map?
What do you mean by chromatic number?

SECTION-B

Give the properties of relations and functions?
Prove that a graph G with e=v-1 that has no circuit is a tree.
How eulerian chains and cycles are related to a connected graph?
Let a, b be elements of a Boolean algebra then show that a'b' + ab + a'b = a'+b.

SECTION-C

Discuss Pigeon Hole Principle in combinatorial mathematics.
What is a semigroup show for example?
How do you use a graph to solve a coloring problem?
What is the difference between a permutation and a combination? Show with example.

Answers: -

Section A

Q1. Ordered Pair

Ans: - An ordered pair refers to a number written in a certain order. An ordered pair is used to show the position on a graph. where the "x" (horizontal) value is first, and the "y" (vertical) value is second. Also in the cordite system ordered pair is used to locate a point.

ordered pair = (x, y)

An ordered pair consists of two numbers that are written in a fixed order. So, we can define an ordered pair as the pair of elements that occur in a particular order and are enclosed in brackets.

Example: -

= (2, 5)

The ordered pair (2, 5) means a pair of two integers, strictly in the order with 2 at the first place called the abscissa and 5 at the second place called the ordinate.

The ordered pair (2, 5) is not equal to the ordered pair (5, 2) because (2, 5) ≠ (5, 2)

Q2. Hashing function

Ans: - The hash function is a function that is applied on a key by which it produces an integer, which can be used as an address of the hash table. Hence one can use the same hash function for accessing the data from the hash table. In this, the integer returned by the hash function is called the hash key. A hash function is a function or algorithm that is used to generate the encrypted or shortened value to any given key.

Example: -

Q3. Rings

Ans: - An algebraic system <R, +, • >, where R is a non-empty set, ‘+’ and ‘•’ Two binary compositions defined onset R is called a ring if.

(R, +) is Abelian group

(a+b)+c = a+(b+c) for all a,b,c ∊ R
a+b = b+a for all a,b ∊ R
for all a ∊ R, - a ∊ R, such that a+(-a) = 0
for all a ∊ R, o ∊ R such that a + o = a

(R, •) is semi group

(ab)c = a(bc)

Distributev Law

{a(b+c) = ab + ac} and {(a+b)c = ac + bc} for all a,b,c ∊ R

Q4. Isomorphic in Graph Theory

Ans: - Graph Isomorphism is a phenomenon of existing the same graph in more than one form. Such graphs are called Isomorphic graphs.

Graph Isomorphism Conditions

The number of vertices in both graphs must be the same.
The number of edges in both graphs must be the same.
The degree sequence of both the graphs must be the same.
If a cycle of length k is formed by the vertices { v1, v2, ….., vk } in one graph, then a cycle of the same length k must be formed by the vertices { f(v1), f(v2), ….., f(vk) } in the other graph as well.

Example: -

Q5. Finite Group

Ans: - A Group (G, *) is called a finite group if G is a finite set.

A finite group is a group having finite group order. Examples of finite groups are the modulo multiplication groups, point groups, cyclic groups, dihedral groups, symmetric groups, alternating groups, and so on.

Example:

The group G = {1, 2, 3, 4, 5, 6, 7} under multiplication modulo 8 is a finite group as the set G is a finite set.

Q6. Principle of Inclusion

Ans: - The Principle of Inclusion-Exclusion (abbreviated PIE) provides an organized method/formula to find the number of elements in the union of a given group of sets, the size of each set, and the size of all possible intersections among the sets.

The principle of inclusion and exclusion (PIE) is a counting technique that computes the number of elements that satisfy at least one of several properties while guaranteeing that elements satisfying more than one property are not counted twice.

In the case of objects being separated into two (possibly disjoint) sets, the principle of inclusion and exclusion states

∣A∪B∣=∣A∣+∣B∣−∣A∩B∣,

To prove this statement, we will show that every element which belongs in one of these sets is counted exactly once, and every element that is not in these sets is counted exactly zero times.

Case 1. Element is not in AA, and not in BB. It is obvious it is counted zero times in the LHS. It is obvious it is counted zero times in the RHS.
Case 2. Element is in AA, and not in BB. It will be counted once on the LHS. On the RHS, it is counted once in |A|∣A∣.
Case 3. Element is not in AA and is in BB. It will be counted once on the LHS. On the RHS, it is counted once in |B|∣B∣.
Case 4. Element is in AA, and in BB. It will be counted once on the LHS. On the RHS, it is counted +1+1 in |A|∣A∣, +1+1 in |B|∣B∣ , and -1−1 in |A \cap B |∣A∩B∣. Hence, it is counted exactly once.

As a Venn diagram, PIE for two sets can be depicted easily:

Q7. Undirected Graph

Ans: - Undirected graphs have edges that do not have a direction. The edges indicate a two-way relationship, in that each edge can be traversed in both directions. This figure shows a simple undirected graph

Q8. Indegree of Graph

Ans: - Indegree of vertex V is the number of edges that are coming into the vertex V. Notation − deg−(V)

Example: -

In-degree of vertex 0 = 0
In-degree of vertex 1 = 1
In-degree of vertex 2 = 1
In-degree of vertex 3 = 3
In-degree of vertex 4 = 2

Q9. Karnaugh Map

Ans: - In many digital circuits and practical problems we need to find expression with minimum variables. We can minimize Boolean expressions of 3, 4 variables very easily using K-map without using any Boolean algebra theorems. K-map can take two forms Sum of Product (SOP) and Product of Sum (POS) according to the need of the problem. K-map is a table-like representation but it gives more information than TRUTH TABLE. We fill the grid of K-map with 0’s and 1’s then solve it by making groups.

Steps to solve expression using K-map-

Select K-map according to the number of variables.
Identify minterms or maxterms as given in the problem.
For SOP put 1’s in blocks of K-map respective to the minterms (0’s elsewhere).
For POS put 0’s in blocks of K-map respective to the maxterms(1’s elsewhere).
Make rectangular groups containing total terms in the power of two like 2,4,8 ..(except 1) and try to cover as many elements as you can in one group.
From the groups made in step 5 find the product terms and sum them up for SOP form.

Example: Minimize the following Boolean Expression using k-map:

AB + A' B+BA'

Draw the two-variable k-map and insert 1's in the corresponding cells as shown in fig:

The required minimized Boolean Expression is f = A + B.

Q10. Chromatic Number

Ans: - The minimum number of colors required for vertex coloring of graph ‘G’ is called the chromatic number of G, denoted by X(G). X(G) = 1 if and only if 'G' is a null graph. If 'G' is not a null graph, then X(G) ≥ 2.

Example: -

(Section B)

Q1. Give the properties of relations and functions?

Ans: -

Properties of Relations: -

Reflexive Relation: - If every element of set A maps for itself, then set A is known as a reflexive relation.

Symmetric Relation: - A relation R on a set is said to be symmetric iff

Transitive relation: - A relation R on a set A is said to be transitive iff

Irreflexive Relation: -

Antisymmetric Relation: -

Asymmetric Relation: -

Identity relation: -

Void Relation: -

Properties of function: -

One-to-One (Injective): - One element of the Domain set is connected to one element of the Co-Domain set.

Onto (Surjective): - Every element of the Co-domain set have one pre-image.

Bijective (1:1 and onto): -

Into: - If there exists even a single element in B having no pre-image in a, then f is said to be an into function. Clearly, f is a function from A to B. Now, there exists an element C <- B, having no pre-image in A. so, f is an into function.

One-one into: - f x -> y. The function f is called one-one into a function if different elements of x have different unique images of y.
Many-one function: - If two or more than two elements of the domain have the same image in B, then f is said to be many – one.
Many-one into a function: - The function f is called the many – one function if and only if is both many one and into function.
Many-one onto function: - The function f is called many-one onto function if and only if is both many one and onto.
Identity function: - The function f is called the identity function if each element of set A has an image on itself.

Q2. Prove that a graph G with e=v-1 that has no circuit is a tree.

Ans: -

To Prove: -

G is a Tree

i.e. G is connected and circuit less.

Suppose G has a circuit, for two vertices a and b, in which there are 2 different paths between them & since G is connected, so no. of edges is greater than (>) n-1.

∴ →← n-1 edges.

∴ G is connected and circuit less (i.e.) G is a Tree

(OR)

Let us Prove by Contradiction.

Assume G contains circuits,

Remove an edge from the circuit so that the resulting graph is again connected.

continue this process of removing one edge from one circuit at a time till the resulting graph -

H is a tree

As H has n vertices, the number of edges it has equals n-1

Now, the number of edges in G is greater than that in

H ⇒ n-1 > n-1,

Which isn't possible

so, G has no circuit

Q3. How eulerian chains and cycles are related to a connected graph?

Ans: -

Euler Graph: - Any connected graph is called an Euler Graph if and only if all its vertices are of even degree.

Example: -

This graph is a connected graph and all its vertices are of even degree.
Therefore, it is an Euler graph.

Euler Chain: - Euler chain is also known as Euler Trail or Euler Walk.

If there exists a walk in the connected graph that visits every edge of the graph exactly once with or without repeating the vertices, then such a walk is called an Euler walk.
Example: -

Euler Cycles: - Euler circuit is also known as Euler Circuit or Euler Tour.

If there exists a chain in the connected graph that starts and ends at the same vertex and visits every edge of the graph exactly once with or without repeating the vertices, then such a walk is called an Euler circuit.
Examples

Q4. Let a, b be elements of a Boolean algebra then show that a'b' + ab + a'b = a'+b.

Ans: - Prove will be to construct a truth table for L.H.S. and R.H.S. and then check for equality

L.H.S. - a'b' + ab + a'b

R.H.S. - a'+b

Section C

Q1. Discuss Pigeon Hole Principle in combinatorial mathematics.

Ans: -

Pigeonhole Principle

The Pigeonhole Principle says that if you have more pigeons than pigeonholes, then at least one pigeonhole will get two pigeons.

If you have a function from a finite set to a smaller finite set, then the function cannot be one-to-one; in other words, there must be at least two elements in the domain with the same image in the codomain.
More formally,

If f:X→Y f:X→Y where XX and YY are finite sets with |X|>|Y||X|>|Y|, then ff is not one-to-one.

Theorem –
If “A” is the average number of pigeons per hole, where A is not an integer then

At least one pigeon hole contains ceil[A] (smallest integer greater than or equal to A) pigeons
Remaining pigeon holes contains at most floor[A] (largest integer less than or equal to A) pigeons

We can say as, if n + 1 objects are put into n boxes, then at least one box contains two or more objects. The abstract formulation of the principle: Let X and Y be finite sets and let be a function.

If X has more elements than Y, then f is not one-to-one.
If X and Y have the same number of elements and f is onto, then f is one-to-one.
If X and Y have the same number of elements and f is one-to-one, then f is onto.

The pigeonhole principle is one of the simplest but most useful ideas in mathematics. We will see more applications than proof of this theorem.
Example: – A bag contains 10 red marbles, 10 white marbles, and 10 blue marbles. What is the minimum no. of marbles you have to choose randomly from the bag to ensure that we get 4 marbles of the same color?
Solution: Apply the pigeonhole principle.

No. of colors (pigeonholes) n = 3
No. of marbles (pigeons) K+1 = 4
Therefore the minimum no. of marbles required = Kn+1
By simplifying we get Kn+1 = 10.
Verification: ceil[Average] is [Kn+1/n] = 4
[Kn+1/3] = 4
Kn+1 = 10
i.e., 3 red + 3 white + 3 blue + 1(red or white or blue) = 10

Q2. What is a semigroup show for example?

Ans: - Semi Group: - Let us consider, an algebraic system (A, *), where * is a binary operation on A. Then, the system (A, *) is said to be semi-group if satisfies the following properties: -

Closure Property: - Let S be a non-empty set, A binary operation * on S is said to be a closed binary operation on S, if

a * b ∊ S, for all a, b ∊ S.

Associative Property: - Let S be a subset of Z. A binary operation * on S is said to be associative, if

(a * b) * c = a * (b * c) for all a, b, c ∊ S

Example: Consider an algebraic system (A, *), where A = {1, 3, 5, 7, 9....}, the set of positive odd integers and * is a binary operation that means multiplication. Determine whether (A, *) is a semi-group.
Solution:

Closure Property: The operation * is a closed operation because multiplication of two +ve odd integers is a +ve odd number.
Associative Property: The operation * is an associative operation on set A. Since every a, b, c ∈ A, we have

(a * b) * c = a * (b * c)

Hence, the algebraic system (A, *), is a semigroup.

Q3. How do you use a graph to solve a coloring problem?

Ans: - Graph Coloring - Graph Coloring is a process of assigning colors to the vertices of a graph such that no two adjacent vertices of it are assigned the same color.

Graph Coloring Algorithm-

There exists no efficient algorithm for coloring a graph with a minimum number of colors.
Graph Coloring is an NP-complete problem.
However, the following greedy algorithm is known for finding the chromatic number of any given graph.

Greedy Algorithm-

Step-01: Color the first vertex with the first color.
Step-02: Now, consider the remaining (V-1) vertices one by one and do the following-

Color the currently picked vertex with the lowest numbered color if it has not been used to color any of its adjacent vertices.
If it has been used, then choose the next least numbered color.
If all the previously used colors have been used, then assign a new color to the currently picked vertex.

Example:

Find the chromatic number of the following graph-

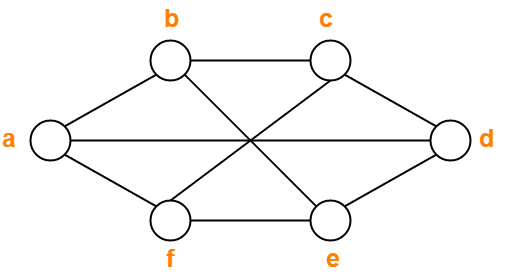
Solution- Applying Greedy Algorithm, we have-

From here,

The minimum number of colors used to color the given graph are 2.
Therefore, the Chromatic Number of the given graph = 2.

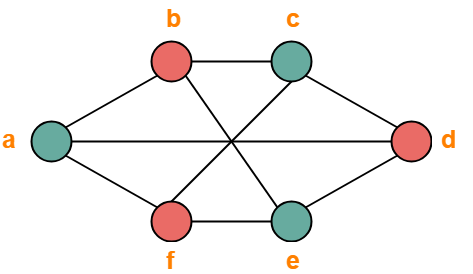
The given graph may be properly colored using 2 colors as shown below-

Q4. What is the difference between a permutation and a combination? Show with example.

Ans: Permutation: Permutation can simply be defined as the several ways of arranging a few or all members within a specific order. It is the process of legibly arranging from chaos. This is what is termed a Permutation.

Combination: The combination is a process of selecting the objects or items from a set or the collection of objects, such that (unlike permutations) the order of selection of objects does not matter. It refers to the combination of N things taken from a group of K at a time without repetition.

Example: - Suppose, we have to find the total number of probable samples of two out of three objects X, Y, Z. Here, first of all, you have to understand whether the problem is relevant to permutation or combination. The only means to find it is to check whether the order is necessary or not.

If the order is important, then the problem is related to permutation, and the possible number of samples will be, XY, YX, YZ, ZY, XZ, ZX. In this case, XY is distinct from the sample YX, YZ is distinct from the sample ZY and XZ is distinct from the sample ZX.

If the order is unnecessary, then the question is relevant to the combination, and the possible samples will be XY, YZ, and ZX.

Top

Search This Blog

mk7 question paper